对约束满足问题的解决方法，包括BT、FC、MRV、GAC。

• BT
• FC
• MRV
• GAC

information

一个约束满足问题（CSP）具备以下性质：

• 一系列变量V1……Vn
• 每个变量Vi有多个取值的可能，记为域Di
• 每个变量Vi有其约束条件Ci

约束满足问题的解：

• 每个变量都已取值
• 对于每个变量Vi，其约束条件Ci都能得到满足

---

BT

Back Tracking，即回溯算法。

• 算法思路
  尝试从剩余未取值变量的选取一个Vi，依次对其赋予Di中的值d。
  • 若与已填充值发生冲突，则代表在此刻、对于Vi，不该填充该值d，则进行下一次取值尝试
  • 若Di中的所有值都不可取，则意味着当前状态下的CSP是无解的，亦即上一个取值Vj是不合理的
  • 否则，以Vi=d的条件下继续下一次赋值
• 伪代码

  BT(level):
      if all V is assigned:
          we get a solution
          return True
      Pick a unassigned Vi
      Di = Domain(Vi)
      Assigned[Vi] = True
      for d in Di:
          Vi = d
          Valid = True
          for all other Assigned Vj:
              if (C(Vj, Vi) is not OK):
                  Valid = False
                  Break
          if Valid:
              BT(level + 1)
      Assigned[Vi] = False
      return False
  

---

FC

Forward Checking，即前向检测

• 算法思路
  该算法基于回溯算法，弥补了回溯算法的一些缺点。
  分析以下情况：
  
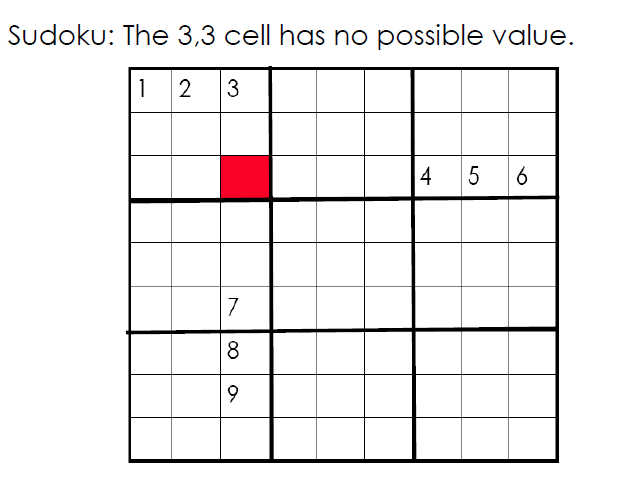
  图中红点处是无值可取的，然而，只是使用回溯算法的话，要一直遍历该点前的所有变量Vi和其所有的值Di才能判断该CSP是无解的。
  若是我们在遍历过程中，能够知道某个变量Vi的作用域Di为空，就可以提前知道当前CSP状态是无解的，也就是这里的Forward Checking。
• 伪代码

  FC_UPDATE(Vi):
      for Vi's all other relative and unAssigned Vj:
          Dj = Domain(Vj)
          for p_d in Dj:
              if 'Vj = p_d' makes C(Vi, Vj) is not OK:
                  remove p_d from Dj
          if Dj is empty:
              FC_UPDATE is not OK
              return False
      FC_UPDATE is OK
      return True
  FC(level)
      if all V is assigned:
          we get a solution
          return True
      Pick a unassigned Vi
      Di = Domain(Vi)
      Assigned[Vi] = True
      for d in Di:
          Vi = d
          dwo_occured = (FC_UPDATE(Vi) is not OK)?
          if (dwo_occured):
              ResotreAllDomainChangedByFC_UPDATE();
          else:
              FC(level + 1)
      Assigned[Vi] = False
      return False
  

MRV

Minimum Remaining Values Heuristics
这是一种策略，即在所有未赋值变量Vi中，选取Di的长度最小的那个Vi作为下一个赋值变量。
原理是减小节点展开次数，提高搜索效率。

GAC

Generalized Arc Consistency

• 算法原理
  个人理解，这是对FC的优化。GAC通过一些逻辑错误来减少更多的节点。
  首先，我们称Vi是一致的，当且仅当对Di中的任意一个值，Dj都存在一个值使得C(X, Vj…)是满足的。
  则，若Di中的某个值d不能满足这种要求，赋予Vi这个值将无法使得所有V都被赋值，亦即此时d是可以被删除的。
• 伪代码

  GAC_ENFORCE(Vi):
      all_consistent = True
      queue = all relative and unAssigned Vj of Vi
      and queue is non-repeatable
      while queue not Empty:
          pick a Vj in queue
          Dj = Dom(Vj)
          Vj_consistent = True
          for d in Dj:
              for all relative and unAssigned Vk of Vj:
                  if Vk has not possible value make C(Vj, Vk) OK:
                      remove d in Dj
                      Vj_consistent = False
                      if Vj becomes Empty:
                          GAC_ENFORCE is not OK
                          return False
          if (!Vj_consistent):
              push all relative and unAssigned Vk of Vj into queue
          GAC_ENFORCE is OK
          return True
  GAC(Level):
      if all V is assigned:
          we get a solution
          return True
      Pick a unassigned Vi
      Di = Domain(Vi)
      Assigned[Vi] = True
      for d in Di:
          Vi = d
          dwo_occured = (FC_UPDATE(Vi) is not OK)? || (GAC_ENFORCE(Vi) is not OK)?
          if (dwo_occured):
              ResotreAllDomainChanged();
          else:
              FC(level + 1)
      Vi = Empty
      Assigned[Vi] = False
      return False