- 简介
使用Minimax strategy对两人对弈的零和的有穷状态问题进行搜索并对其进行alpha-beta剪枝。
- 思路
我们知道,这类型的博弈有以下性质- 状态集是有限的
- 目标状态是可分辨的
- 目标状态是可评估的
那么,所有状态的评估值都可使用Minimax strategy由目标节点倒推而出,
若是MAX方,则其可到达的最大节点为其后继节点的最大值,若为MIN方,则其可到达的最大节点为其后继节点的最小值 - 伪代码
DFS(node, isMax, successors): if (node is target): return value of node next_nodes = successors of node value = isMax ? -infinite : infinite; for next_node in next_nodes: if (isMax): value = max( value, DFS(next_node, successors, !isMax) ) else: value = min( value, DFS(next_node, successors, !isMax) ) return value
- alpha-beta剪枝
- 概述
由于使用的是深度遍历搜索,则我们会从左往右遍历每一片叶子。对于每一个非叶子节点,其值的获取都需要子节点遍历结束,然而,这一过程往往是不必要的。
举个例子:
A节点有两个子节点B1、B2,B1、B2又有分别两个子节点C1、C2和D1、D2,假设C、D为目标节点。
那么,由于是博弈搜索,则若A是Max节点,则B为Min节点。
A在遍历完B1的所有子节点时会得到一个alpha值,则有A的值大于等于alpha值(Max)。
现在我们遍历B2点,
我们遍历B2的子节点D1时会得到一个beta值,则有B的值小于等于beta值(Min)。
若beta <= alpha,则得到关系
val(A) >= alpha >= beta >= val(B)
于是,D2节点的遍历与否只能影响val(B)而将不能影响到A的值,那么若我们只关心A节点的值,就可以把B节点的遍历终止掉。
到这里是没有问题的,现在有个地方可以讨论下,父节点(Max)的alpha值能否影响不止一代的子节点(Min)?
答案是可以的,如 A(Max) -> B(Min) -> C(Max) -> D(Min)
我们有val(A) >= val(B); val(C) >= val(D); val(B) <= val(C);
若beta(D) <= alpha(A),则由val(C) >= val(D)可得:- val(C) > val(D):
D是可忽略的
- val(C) == val(D):
则val(B) <= ( val(C) == beta(D) ) <= alpha(A) <= val(A)
那么B是可忽略的(直系子元素),也就意味着D是可忽略的
证毕 - val(C) > val(D):
- 伪代码
AlphaBeta(node, isMax, successors, alpha=-infinite, beta=infinite): if (node is target): return value of node next_nodes = successors of node for next_node in next_nodes: if (isMax): alpha = max( alpha, AlphaBeta(next_node, !isMax, successors, alpha, beta) ) else: beta = min( beta, AlphaBeta(next_node, !isMax, successors, alpha, beta) ) if (beta <= alpha): break return isMax ? alpha : beta
- 概述
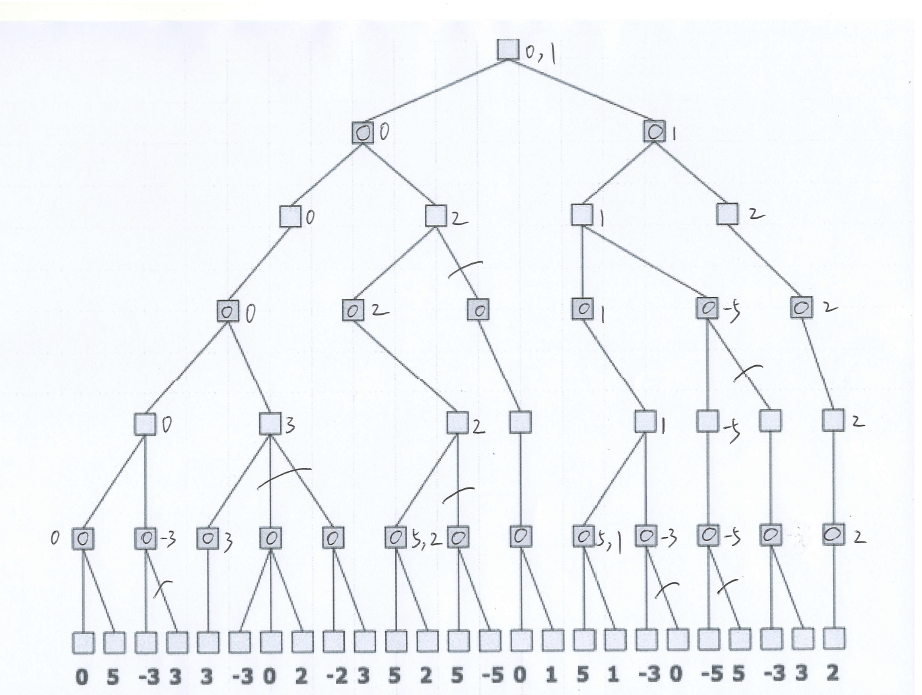
- Result