• Problem

  
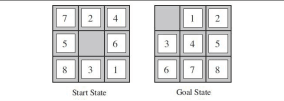
  如图，通过A*算法求出最优解法

• Code

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>
#include <functional>
#include <string>
#include "math.h"
#include <ctime>
#include <cstdlib>
using namespace std;
int direction[][2] = {
    { 0, -1 },
    { 0, 1 },
    { 1, 0 },
    { -1, 0 }
}, maxCost = 30;
class node {
public:
    node(int* begin=nullptr) : val(9, -1) {
        init(begin);
    }

    void init(const int* begin) {
        blackPos = -1;
        fn = 0;
        cost = 0;
        path = "";
        if (begin) {
            for (int i = 0; i < 9; i++) {
                val[i] = begin[i];
                if (!val[i]) {
                    blackPos = i;
                }
            }
        }

    }

    string toString() {
        string str = "";
        for (int i = 0; i < 9; i++) {
            str += val[i] ? val[i] + '0' : ' ';
            str += " ";
            if ((i + 1) % 3 == 0) {
                str += "\n";
            }
        }
        return str;
    }

    bool equal(const node& target) {
        for (int i = 0; i < 9; i++) {
            if (val[i] != target.val[i]) {
                return false;
            }
        }
        return true;
    }

    int hn(const node& target) {
        int dis = 0, sum = 9, index[9];

        for (int i = 0; i < 9; i++) {
            index[target.val[i]] = i;
        }
        for (int i = 0; i < 9; i++) {
            int value = val[i];
            dis = abs(i / 3 - index[value] / 3) + abs(i % 3 - index[value] % 3);
            sum += dis;
        }

        return cost + sum - 1;
    }
    string getPath() {
        return path + "->\n" + toString();
    }
    node move(int i) {
        int nextX = blackPos / 3 + direction[i][0],
            nextY = blackPos % 3 + direction[i][1];
        node next = *this;
        next.cost = cost + 1;
        next.path = getPath();
        if (nextX < 0 || nextY < 0 || nextX > 2 || nextY > 2) {
            next.cost = -1;
        }
        else {
            next.blackPos = nextX * 3 + nextY;
            next.val[blackPos] = next.val[next.blackPos];
            next.val[next.blackPos] = 0;
        }
        return next;
    }

    vector<int> val;
    int blackPos;
    int cost;
    int fn;
    string path;
};

pair<int, string> search(const node &start, const node &target) {
    std::vector<node> q;
    unordered_map<string, int> closet;
    q.push_back(start);
    while (!q.empty()) {
        node cur = q[0];
        q.erase(q.begin());
        if (cur.equal(target)) {
            return make_pair(cur.cost, cur.getPath());
        }
        closet[cur.toString()] = cur.cost;
        for (int i = 0; i < 4; i++) {
            node next = cur.move(i);
            string key = next.toString();
            if (next.cost < maxCost && next.cost != -1 && (closet.find(key) == closet.end() || closet[key] > next.cost)) {
                next.fn = next.hn(target);
                q.push_back(next);
            }
        }
        sort(q.begin(), q.end(), [&](const node &a, const node &b) {
            return a.fn < b.fn;
        });
    }
    return make_pair(-1, "couldn't find");
}

int main() {
    int a[9] = { 7, 2, 4, 5, 0, 6, 8, 3, 1 },
        b[9] = { 0, 1, 2, 3, 4, 5, 6, 7, 8 };
    node start(a), end(b), randomMap = end;

    /*
        随机puzzle生成
        srand(unsigned(time(0)));
        int randomSize = rand() % 10000;
        for (int i = 0; i < randomSize; i++) {
            int j = rand() % 4;
            node next = randomMap.move(j);
            if (next.cost != -1) {
                randomMap = next;
            }
        }
        start = randomMap;
    */
    start.cost = 0;
    start.path = "";

    cout << "from \n" << start.toString() << "to\n" << end.toString() << "cost ";
    auto t = search(start, end);
    cout << t.first << " steps\n" << t.second << endl;
    return 0;
}

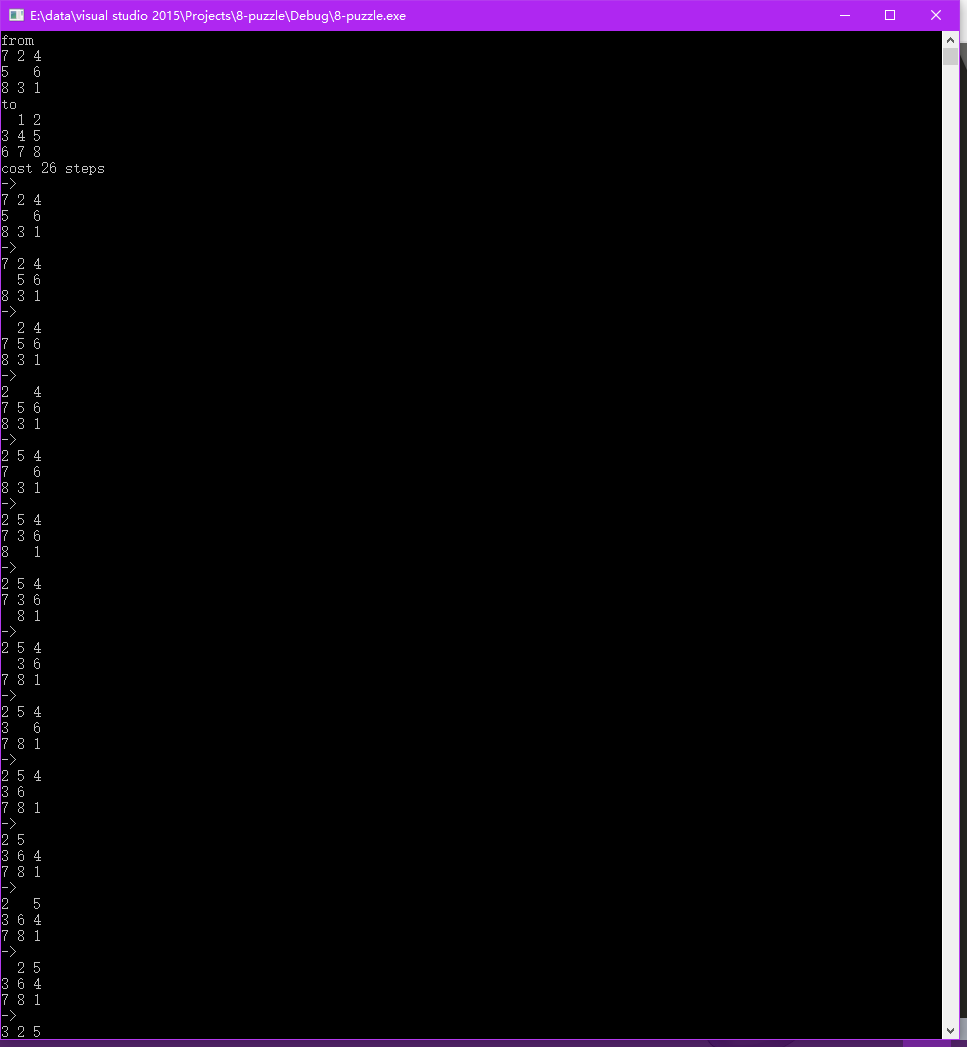
• Result

  

• 备注

  • 关于上面代码中的maxCost变量，这主要是我观察了多个puzzle的搜索结果，发现他们的步骤都小于30，于是进行了大胆的猜想，正确性未知。
    不过，由此想到了迭代加深算法，我们可以把每次被maxCost砍掉的节点保存下来，然后如果在当前maxCost下未找到结果，则maxCost加大，再从这些被砍掉的节点处重新开始

  • 关于 h(n) 为什么是cost + sum。
    若 h(n) 只有sum来决定，则会出现这种情况，当cost对结果的影响超过sum时，将因为缺失对cost的判断而导致求出的解有可能不是最优解。