介绍一些图的性质，比如有向图中的树边、回边、横边、前向边、强连通分量等。

有向图

• 有向图的遍历 DFS

  counter = 1, records = {}, prev = {}, post = {}
  TreeSearch(nodes, map):
      for cur_node in nodes:
          if (records.has(cur_node)):
              ignore cur_node
          else:
              records[cur_node]
  
          prev[cur_node] = counter
          add counter
  
          next_nodes = map[nodes]
          TreeSearch(next, map)
  
          post[nodes] = counter
          add counter
  

  上面的遍历与常规 DFS 差不多，只不过在遍历过程中对每个节点进行了遍历先后顺序的记录。那么记录这些节点访问顺序的先后有什么用呢？

  
  这里介绍一些概念
  

  
  

  根节点

  
  

  即一棵搜索树中第一个遍历的节点

  
  

  祖先节点

  
  

  节点A在不停的往上回溯直至根节点停止的过程中所访问的节点均为A的祖先节点

  
  

  后代节点

  
  

  所有以节点A为根节点的节点均为A的后代节点

  
  

  树边

  
  

  若通过节点A访问了节点B且节点B未被访问过，则 A -> B 为一条树边

  
  

  回边

  
  

  若通过节点A访问了节点B且节点B为节点A的祖先节点，则 A -> B 为一条回边

  
  

  前向边

  
  

  若通过节点A访问了一个已被访问过的节点B，并且节点B为节点A的后代节点，则 A -> B 为一条前向边

  
  

  横边

  
  

  若通过节点A访问了一个已被访问过的节点B，并且节点B不为节点A的祖先、后代节点，则 A -> B 为一条横边

  
  

  
  上图（图是偷来的）
  
  

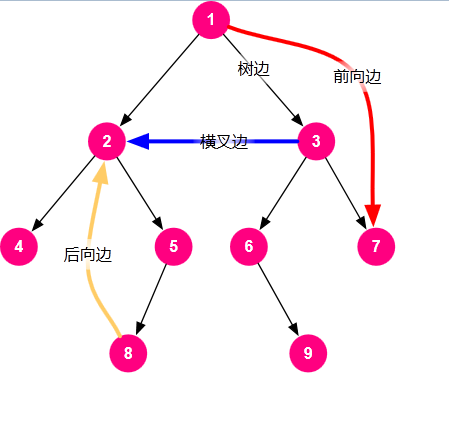
  接下来，通过各种边的性质我们可以知道

  • 树边 u -> v
    先访问u，再访问v且v未被访问。此时有 prev[u] && !post[u] && !prev[v] && !post[v]
  • 回边 u -> v
    先访问v，再访问u，然后再由u访问v，且此时v的遍历还未结束。此时必有 prev[v] < prev[u] && !post[v] && !post[u]
  • 前向边 u -> v
    先访问u，再通过其他节点访问到v，然后再由u直接访问u，且此时u的遍历还未结束。此时有 prev[u] < prev[v] < post[v] && !post[u]
  • 横边 u -> v
    先访问v，再访问u，然后u访问v，此时v的遍历已结束。此时有 prev[v] < post[v] < pre[u] && !post[u]
  • 总结一下
    在遍历结束后，若 u可到v，则有
    回边: prev[v] < prev[u] < post[u] < post[v] -> [{}]
    树边或者前向边: prev[u] < prev[v] < post[v] < post[u] -> {[]}
    横边: prev[v] < post[v] < prev[u] < post[u] -> []{}
    {: prev[u], }: post[u], [: prev[v], ]:post[v]

• 拓扑排序

  
  对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得排在后面的点没有一条边连着前面的点。
  通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。
  
  • 算法1
    根据概念，首先这是一个无环图，且排在后面的点没有一条边连着前面的点。
    于是，我们对图进行DFS遍历，那么，该图中肯定不存在回边，假设后面的点u有一条边连着前面的点v，则这条边只有以下几种情况：
    树边或者前向边: prev[u] < prev[v] < post[v] < post[u]
    横边: prev[v] < post[v] < prev[u] < post[u]
    不管是哪种情况，都存在 post[v] < post[u]，则只要我们按照post值从大到小排序，就不会出现从后面的点u连着前面的点v这种情况了。从而也就可以得到一个拓扑序列了。

  • 算法2
    引入概念

    
    

    
    

    入度

    进来的边的数量

    
    

    出度

    出去的边的数量

    
    

    源顶点(source)

    入度为0的点

    
    

    汇定点(sink)

    出度为0的点

    
    

    DAG中都存在一个源顶点

    一颗树中总会有一个根节点，若根节点入度也不为0且同时要求这颗树中不存在回边，那就只能是一条横边，该横边必然来源于另外一棵树，然而对于另外一颗树，又要求其根节点入度也不为0，此时又需要另一颗树，如此重复下去将无穷无尽，显然不行。故而DAG中都存在一个源顶点。

    
    

    DAG中都存在一个汇顶点

    一颗树中总会遍历结束，那对于这些位于底端的叶子节点，若其出度不为0且同时要求这颗树中不存在回边，因其位于底端，故而不会有树边和前向边，那么就只能是横边，然而横边指向的是已经遍历结束的、不互为祖先后代的节点，那么，对于第一个位于底端的叶子节点，他必然是第一个遍历结束的点，这时候他又应指向哪个已经遍历结束的节点？故而DAG中都存在一个汇顶点。

    
    

    
    

    入度为0的点肯定就不会存在有其他点指向自己这种情况。于是我们对所有节点都采取以下操作

    1. 若该节点入度为0，则添加到序列中，并将其指向的点的入度减一。

    2. 若在入度减一的节点中出现入度为0，对其进行同样操作。
       这样直到所有节点都被加入序列之后，该序列就是一个拓扑序列。
       有没有可能出现有些点没有被加入序列中，却没有入度为0的点了？

       
       不可能。若出现上面的情况，则意味着存在环。
       

• 强连通分量

  
  有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。
  
  • 强连通分量将图分解成DGA
    若强连通分量不将图分解成DGA，则存在环，那么位于该环上的强连通分量就是互相可抵达的，这与强连通分量是极大的矛盾。
  • 若强连通分量A指向B，则A中post最大的值必然大于B中post最大的值
    • 我们假设深搜时是从A中的某个点开始的，因为B中所有点都是强连通的，故而B中所有点访问结束之后才会借宿A中指向B中的那个点的访问，也就是说此时A中指向B中的那个点的post值将大于B中所有点的post值；
    • 我们假设深搜时是从B中的某个点开始的，因为A指向B且该图是DGA，则B不存在一条路径可以指向A，于是在B中所有可到达的点访问结束后才会对A中的点进行访问，于是A中点的post值将大于B中所有点的post值。

  • post值最大的点必然处于源强连通分量里
    有第2条属性可知，post值最大的点所处的强连通分量入度为0，故而其必然处于源强连通分量里。

    根据上面三条属性，我们可以得到以下的划分方法：

  1. 对图进行深搜，得到每个节点的post值
  2. 将有向图的方向反转，则强连通分量依旧连通，而原图中的源强连通分量变为新图中的汇强连通分量（出度为0），而从汇强连通分量中的点是不会访问到其他强连通分量的点的。
  3. 从post值最大的点对图进行深搜，待搜索结束后将所有遍历的点划为一个强连通分量并从新图中去除，重复步骤3直到图为空。