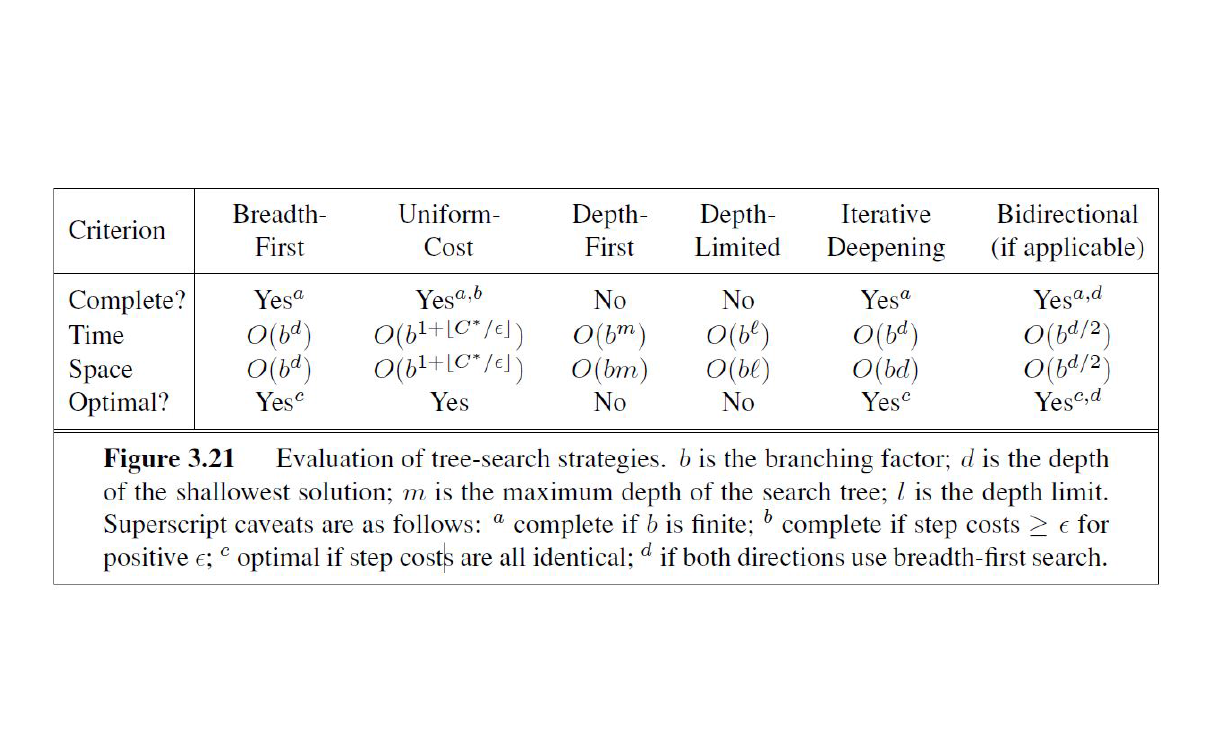
一些搜索算法,包括广搜、深搜、一致代价搜索、深度受限搜索、A*算法
BFS
- 算法思路
从待处理队列中取出第一个节点,若为目标节点则返回该节点,否则,将该节点添加到待处理队列的末尾中。简单地说,广搜是一层一层的对树进行搜索的。
- 伪代码
TreeSearch(Frontier, Sucessors, Goal? )
If Frontier is empty return failure
Curr = select state from Frontier
If (Goal?(Curr)) return Curr.
Frontier’ = (Frontier – {Curr}) U Successors(Curr)
return TreeSearch(Frontier’, Successors, Goal?)
Uniform-Cost
- 算法思路
每次都展开代价最小的节点,当其以深度为代价时,就相当于广搜。
- 伪代码
TreeSearch(Frontier, Sucessors, Goal? )
If Frontier is empty return failure
Curr = select state from Frontier
If (Goal?(Curr)) return Curr.
Frontier’ = (Frontier – {Curr}) U Successors(Curr)
SortByCost(Frontier’)
return TreeSearch(Frontier’, Successors, Goal?)
DFS
- 算法思路
从待处理队列中取出第一个节点,若为目标节点则返回该节点,否则,将该节点添加到待处理队列的开始出。简单地说,广搜是一条一条的对树进行搜索的。
- 伪代码
TreeSearch(Frontier, Sucessors, Goal?)
If Frontier is empty return failure
Curr = select state from Frontier
If (Goal?(Curr)) return Curr.
Result = TreeSearc(Successors(Curr), Successors, Goal?)
If (Result) return Result;
Frontier’ = (Frontier – {Curr})
return TreeSearch(Frontier’, Successors, Goal?)
DLS
- 算法思路
在深搜的基础上加上深度判断
- 伪代码
TreeSearch(Frontier, Sucessors, Goal?, depth, DepthLimit)
If (depth > DepthLimit) return failure
If Frontier is empty return failure
Curr = select state from Frontier
If (Goal?(Curr)) return Curr.
Result = TreeSearc(Successors(Curr), Successors, Goal?, depth + 1, DepthLimit)
If (Result) return Result;
Frontier’ = (Frontier – {Curr})
return TreeSearch(Frontier’, Successors, Goal?, depth, DepthLimit)
Iterative-Deepening search
- 算法思路
深度限制令深度限制从0开始递增对树进行深度受限搜索
- 若搜索到目标节点则返回目标节点
- 若没有节点因深度限制被丢弃,则整个树已搜索完毕,目标节点不存在
- 伪代码
TreeSearch(Frontier, Sucessors, Goal?, depth, DepthLimit, &IsCutOff)
If (depth > DepthLimit)
IsCutOff = True
return failure
If Frontier is empty return failure
Curr = select state from Frontier
If (Goal?(Curr)) return Curr.
Result = TreeSearc(Successors(Curr), Successors, Goal?, depth + 1, DepthLimit)
If (Result) return Result
Frontier’ = (Frontier – {Curr})
return TreeSearch(Frontier’, Successors, Goal?, depth, DepthLimit)
IterativeDeepeningSearch(Frontier, Successors, Goal?)
Depth From 0 to Infinite
IsCutOff = False
Result = TreeSearch(Frontier, Successors, Goal?, 0, DepthLimit, IsCutOff)
If(Result) return Result
Else If (IsCutOff) continue
Else return failure
A-Start Algorithm
A*算法跟一致代价搜索原理类似,只是在一致低价搜索中我们依据代价来对队列进行排序,而A*算法中我们使用函数 f(n) = g(n) + h(n)作为排序依据,其中 g(n) 为当前节点的代价,h(n) 为我们给出的函数,其值为当前节点到达目标节点的估算值。
- 如何保证搜索结果最优?
- 令 m(n) 表示从当前节点到目标节点的最小代价,只要满足h(n) <= m(n) 即可
A*算法的难点在于如何定义评估函数。
- 伪代码
TreeSearch(Frontier, Sucessors, Goal? )
If Frontier is empty return failure
Curr = select state from Frontier
If (Goal?(Curr)) return Curr.
Frontier’ = (Frontier – {Curr}) U Successors(Curr)
SortByFn(Frontier’)
return TreeSearch(Frontier’, Successors, Goal?)